||Simplification d'une Matrice Simple|| RESOLU
||Simplification d'une Matrice Simple|| RESOLU - Aide aux devoirs - Emploi & Etudes
Marsh Posté le 07-11-2008 à 16:57:04
ReplyMarsh Posté le 07-11-2008 à 17:01:45
| rem4108 a écrit : c'est pas 2*x^4*y^2-1 |
oui désolé, j'ai corrigé.
Mais je repose malgré tout ma question, parce que ça me pose problème, et je ne suis pas sûr du résultat.
Marsh Posté le 07-11-2008 à 17:10:33
C'est bizarre, parce que en calculant la matrice hessienne de la fonction f j'obtiens 1) alors que le corrigé me donne le 2) :

Et en calculant un le déterminant en (1,1) j'obtiens 2 nombres différent, ce qui devrait être impossible, puisque le déterminant d'une fonction est unique.
| Citation : La matrice hessienne c'est : |
Message édité par super striker le 07-11-2008 à 17:11:11
Marsh Posté le 07-11-2008 à 17:18:16
Par exemple dans la diagonale ,tu dérives deux fois par x et deux fois par y.
Donc si je prends les deux premiers termes x²+y²
j'aurais 2 et 2 .
Marsh Posté le 07-11-2008 à 17:21:46
| rem4108 a écrit : Par exemple dans la diagonale ,tu dérives deux fois par x et deux fois par y. |
Là dessus je suis d'accord, mais justement puisque tu m'as dit que ma première égalité est bonne pourquoi je ne trouve pas le même résultat en partant de ma deuxième égalité ?? C'est ça que je ne comprends pas.
Message édité par super striker le 07-11-2008 à 17:22:01
Marsh Posté le 07-11-2008 à 17:29:01
Ça na rien à voir.
Pour le calcul du hessien tu dois reprendre ton calcul avant la transformation.
Tu as pu simplifier seulement pour trouver les x et y qui annulent le gradient.
Marsh Posté le 07-11-2008 à 17:31:28
| rem4108 a écrit : Ça na rien à voir. |
Ah d'accord, j'avais le droit de faire cette transformation uniquement parce que c'étais égale à 0.
Désolé, la honte !! ![]()
Mais surtout merci à toi ![]()
Sujets relatifs:
- Microeconomie Simple
- equa dif simple en prépa
- [RESOLU] Calcul mathématique (niveau 2nd environ)
- [Résolu] Casser contrat pendant période d'essai, Assedic ?
- M2 à cergy (M2 +LLM) ou simple M2 à Montpellier en droit des oblig
- IAE ou simple fac
- La Recherche en Informatique, simple question
- Problème avec matrice et système linéaire
- [resolu]Physique hydrolyse d'un ester

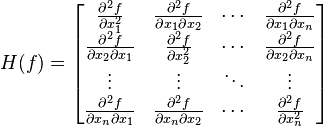
Marsh Posté le 07-11-2008 à 16:34:53
Bonjour,
 J'ai un problème totalement idiot, mais je n'arrive à m'en rendre compte où est mon erreur.
J'ai un problème totalement idiot, mais je n'arrive à m'en rendre compte où est mon erreur.
Je transforme le gradient en :
Première question, est-ce que c'est bon ce que je viens de faire ??
Merci pour votre aide
Edit : Légère correction du gradient de f, mais celà ne change pas le problème
Message édité par super striker le 07-11-2008 à 17:32:07