PHI, le nombre d'or
PHI, le nombre d'or - Sciences - Discussions
Marsh Posté le 11-03-2007 à 19:45:55
à part 2 lettres dans leurs nom (et encore, ça dépend des alphabets), non pas vraiment à ma connaissance
---------------
Celui qui pose une question est idiot 5 minutes. Celui qui n'en pose pas le reste toute sa vie. | Membre du grand complot pharmaceutico-médico-scientifico-judéo-maçonnique.
Marsh Posté le 11-03-2007 à 19:49:11
euh, alors, phi = pi * h
ou alors pi = phi * pi / pi
ou alors plus compliqué (à vérifier) :

EDIT : grilled ![]()
Message édité par asseforever le 11-03-2007 à 19:49:38
Marsh Posté le 11-03-2007 à 19:52:16
| Amapola a écrit : Savez-vous s'il y a un lien entre Pi et Phi ? |
![[:aloy] [:aloy]](https://forum-images.hardware.fr/images/perso/aloy.gif)
Message édité par Amsterd4m le 11-03-2007 à 19:54:27
---------------
Le vice empoisonne le plaisir, la passion le corrompt, la tempérance l'aiguise, l'innocence le purifie, la tendresse le double.
Marsh Posté le 15-03-2007 à 23:14:29
ou alors pi = phi * pi / pi ![]()
---------------
“L'éducation est l'arme la plus puissante que l'on puisse utiliser pour changer le monde”
Marsh Posté le 15-03-2007 à 23:52:24
| kirua_sama a écrit : ou alors pi = phi * pi / pi |
phi = - phi * e^(i*PI) ![]()
---------------
Prévenir HdV en cas d'SQFP ! - Quidquid latine dictum sit, altum sonatur.
Marsh Posté le 17-03-2007 à 00:48:04
ReplyMarsh Posté le 17-03-2007 à 00:57:22
ReplyMarsh Posté le 17-03-2007 à 21:07:21
| Herbert de Vaucanson a écrit : phi = - phi * e^(i*PI) |
---------------
L'APS-C Vaincra :o ├ Galerie ┤ ├ Rome ┤ ├ Belgique ┤
Marsh Posté le 17-03-2007 à 21:28:28
Peux-tu m'expliquer pourquoi le signe PHI est-il à la puissance 0! (zéro factorielle) alors que 0! = 1 ?
Message édité par lLoon le 17-03-2007 à 21:28:51
Marsh Posté le 17-03-2007 à 21:31:53
Ben justement, pour faire 1 ![]()
Non, mais cette équation, c'est 0=0 hein ![]()
Message édité par isofouet le 17-03-2007 à 21:32:19
---------------
L'APS-C Vaincra :o ├ Galerie ┤ ├ Rome ┤ ├ Belgique ┤
Marsh Posté le 18-03-2007 à 18:17:22
Non, non, la formule nous apprend plus de chose que le simple 0=0, elle dit aussi implicitement que Phi > 0.
(ça tombe bien parce que Phi est justement définie comme l'unique solution positive d'une équation du second degré ![]() )
)
Marsh Posté le 18-03-2007 à 18:45:13
Ah oui, exact, le log la définit sur R+*
Enfin bon, on s'en fout un peu en même temps ![]()
---------------
L'APS-C Vaincra :o ├ Galerie ┤ ├ Rome ┤ ├ Belgique ┤
Marsh Posté le 19-03-2007 à 20:09:35
| Herbert de Vaucanson a écrit : phi = - phi * e^(i*PI) |
![]() mon message etait un quote hein....
mon message etait un quote hein.... ![]()
---------------
“L'éducation est l'arme la plus puissante que l'on puisse utiliser pour changer le monde”
Marsh Posté le 20-03-2007 à 02:47:08
| kirua_sama a écrit :
|
Mon message finissait par ":o" hein... ![]()
---------------
Prévenir HdV en cas d'SQFP ! - Quidquid latine dictum sit, altum sonatur.
Marsh Posté le 20-03-2007 à 03:31:28
| Amapola a écrit : tu sais s'il y a un lien entre Pi et Phi ? |
Ouais, même que la clef de tout ça se trouve aux Philippines.
---------------
Technique maquereau | ECNSP | Fructifier son argent avec les branques
Marsh Posté le 05-06-2007 à 11:26:40
bonjour
pour info, j'ai vue sur www.baglis.tv une conférence audio très intéressante car hyper-documentée de Michel Léger sur le nombre d'or. Voici l'adresse:
http://www.baglis.tv/weblog/fiches [...] udio).html
c'est rare de pouvoir entendre des auteurs / conférenciers nous parler calmement et simplement d'un sujet quand c'est aussi pointu. Dites-moi ce que vous en pensez.
Marsh Posté le 08-06-2007 à 00:26:34
| Amapola a écrit : un lien entre Pi et Phi ? |
phi = 2 cos (pi / 5)
Message édité par xantox le 08-06-2007 à 02:18:59
---------------
-- Parcours Etranges : Physique, Calcul, Philosophie
Marsh Posté le 16-06-2007 à 22:41:20
Vive le nombre d'or ! ![[:roi] [:roi]](https://forum-images.hardware.fr/images/perso/roi.gif)
Message édité par ddst le 16-06-2007 à 22:41:45
Sujets relatifs:
- Pourquoi les mois n'ont til pas le même nombre de jour ?
- Nombre de maillots vus dans la rue
- En neuf ans le nombre de chômeurs n'a pas baissé en France
- Confusion sur les nombre de virgule flottantes
- nombre de kms moyen d'une 205 diesel
- Que pensez vous du nombre de fonctionnaires en France?
- Maths : tirer un nombre alétoire selon une loi expo ou poisso
- incidence du nombre de recepteur TV sur un signal d'antenne
- recherche de nombre premier sur le net (renuméré)
- Recherche DVD sous-titré dans un grand nombre de langue

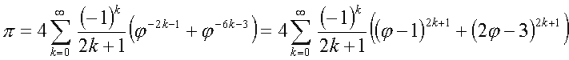
![[:dawa] [:dawa]](https://forum-images.hardware.fr/images/perso/dawa.gif)
![[:scorpio06] [:scorpio06]](https://forum-images.hardware.fr/images/perso/scorpio06.gif)

Marsh Posté le 11-03-2007 à 19:44:38
tu sais s'il y a un lien entre Pi et Phi ?

(nombre PHI dont il est fait référence dans "Da Vinci code " )